Mathématiques pour les mordus

Nouveautés

Trefoil knot conways game of life En topologie, une branche des mathématiques, le noeud du trèfle est l'exemple le plus simple d'un nœud non triviale. Le trèfle peut être obtenu en réunissant les deux extrémités libres d'un noeud commun, ce qui entraîne une boucle nouée. En tant que noeud le plus simple, le trèfle est fondamental pour l'étude de la théorie des noeuds mathématiques.

Lire la suite : Noeud de trèfle

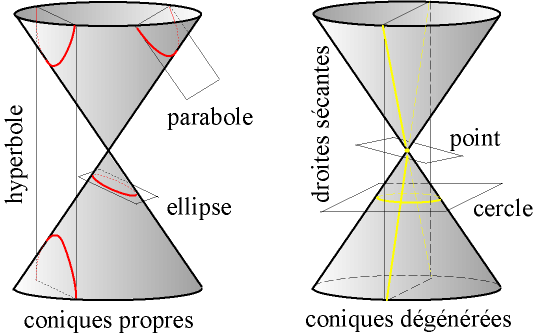Coniques cone Équation du cercle : \((x-h)^2+(y-k)^2=r^2\)

Équation de l'ellipse : \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1\)

Équation de l'hyperbole (horizontale) : \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1\)

Équation de l'hyperbole (verticale) : \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=-1\)

Équation de la parabole : \(y = a(x-h)^2+k\)

Lire la suite : Les coniques

Evariste galois Évariste Galois est un mathématicien français, né le 25 octobre 1811 à Bourg-la-Reine et mort le 31 mai 1832 à Paris. Il a donné son nom à une branche des mathématiques dont il a posé les prémisses, la théorie de Galois. Il est un précurseur dans la notion de groupe et un des premiers à mettre en évidence la correspondance entre symétries et invariants¹. Sa « théorie de l'ambiguïté » est toujours féconde au XXI^e siècle². Elle a ainsi permis, par exemple, à Felix Klein d'élaborer en 1877 la théorie des revêtements puis à Alexandre Grothendieck, en 1960, de fusionner théorie de Galois et théorie des revêtements³.