Mat 4171 - Solution d'une inéquation générale du second degré

Accès membre
Devenir membre

Nouveautés

No posts to display.

Recommander

Solution d'une inéquation générale du second degré

Average rating

1
2
3
4
5

Categories

Mat 4171 | Mat 4161 | Mat 4151

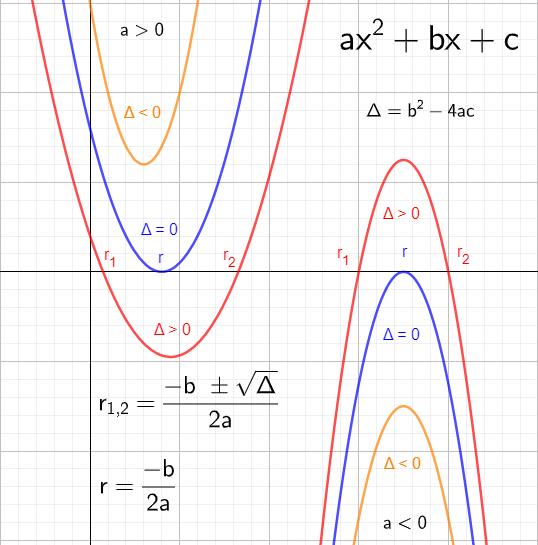
Voici un résumé des solutions possibles pour une inéquation du second degré. Il est intéressant de remarquer la symétrie.

Solutions d'une inéquation du second degré

		\(ax^2+bx+c \geq 0\)	\(ax^2+bx+c > 0\)	\(ax^2+bx+c < 0\)	\(ax^2+bx+c \leq 0\)
\(a > 0\)	\(\Delta > 0\)	\(\begin{array}{l} x \in \mathbb{R} \setminus \left] r_1, r_2 \right[ \\ \mbox{ou} \\ x \in \left] -\infty, r_1 \right] \cup \left[ r_2, \infty \right[ \end{array}\)	\(\begin{array}{l} x \in \mathbb{R} \setminus \left[ r_1, r_2 \right] \\ \mbox{ou} \\ x \in \left] -\infty, r_1 \right[ \cup \left] r_2, \infty \right[ \end{array}\)	\(x \in \left] r_1, r_2 \right[\)	\(x \in \left[ r_1, r_2 \right]\)
	\(\Delta = 0\)	\(x \in \mathbb{R}\)	\(x \in \mathbb{R} \setminus \left\{ r \right\}\)	\(\emptyset\)	\(x \in \left\{ r \right\}\)
	\(\Delta < 0\)	\(x \in \mathbb{R}\)	\(x \in \mathbb{R}\)	\(\emptyset\)	\(\emptyset\)
\(a < 0\)	\(\Delta < 0\)	\(\emptyset\)	\(\emptyset\)	\(x \in \mathbb{R}\)	\(x \in \mathbb{R}\)
	\(\Delta = 0\)	\(x \in \left\{ r \right\}\)	\(\emptyset\)	\(x \in \mathbb{R} \setminus \left\{ r \right\}\)	\(x \in \mathbb{R}\)
	\(\Delta > 0\)	\(x \in \left[ r_1, r_2 \right]\)	\(x \in \left] r_1, r_2 \right[\)	\(\begin{array}{l} x \in \mathbb{R} \setminus \left[ r_1, r_2 \right] \\ \mbox{ou} \\ x \in \left] -\infty, r_1 \right[ \cup \left] r_2, \infty \right[ \end{array}\)	\(\begin{array}{l} x \in \mathbb{R} \setminus \left] r_1, r_2 \right[ \\ \mbox{ou} \\ x \in \left] -\infty, r_1 \right] \cup \left[ r_2, \infty \right[ \end{array}\)

casParabole

Pour une version imprimable, utliser le lien suivant :

Created
mardi 26 avril 2022
Created by
Normand Brousseau
Last modified
mercredi 3 août 2022
Hits
774 views

Mathématiques

Cours de mathématiques

Apprendre plus...

Matériels développés par des enseignants et rendus disponibles pour différents cours de mathématiques.

Passion Maths

Passion Maths

Cogiter plus...

Pour les accrocs... On retrouvera ici tout ce qui fait la beauté des maths... Oui oui, les maths c'est BEAU !

Ultime frontière

Un clin d'oeil à l'univers...

Certaines vidéos de cette section sauront vous captiver !

Informatique

Ne pas éviter les TIC !

Découvrir plus...

Cette section est dédié aux partages des ressources et connaissances TIC dans l'enseignement...

Forum

Discussion et Partage !

Partager plus...

La seule ressource qui se multiplie quand on la consomme, c'est le savoir ! Allez et multipliez-vous !

Documents

Documents

Divers documents relatifs aux mathématiques et aux sciences

Longueuil, Québec, Canada
Tel: (514) 249-6985
Email: Cette adresse courriel est protégée contre les robots spammeurs. Vous devez activer le JavaScript pour la visualiser.

Partout sur le site sauf où expressément indiqué :

Attribution - Partage dans les Mêmes Conditions
CC BY-SA

Ce site utilise des cookies pour vous assurer d'obtenir la meilleure expérience sur notre site, pour suivre l'utilisation de notre site (Google Analytics) et pour financer notre site (Google AdSense).