Monenclature

On utilisera la monenclature suivante.

On dénotera les sommets du triangle et, par extension l'angle associé, par une lettre majuscule. On dénotera le coté opposé à l'angle (représenté par la lettre de son sommet) par la lettre minuscule correspondante. On placera toujours la lettre du sommet opposé à l'angle droit (au plus grand angle) dans le centre de la triade des lettres des sommets.

Par exemple, dans le triangle \(\color {green} \Delta ABC\), le sommet \(B\) est associé à l'angle droit.

Définition

On dit que deux triangles sont semblables s'ils ont la même forme mais pas nécessairement la même taille.

Définition

Dans deux triangles semblables, les cotés homologues sont les cotés qui sont opposés aux mêmes angles.

Formalisation

Voici deux des formalisations les plus courantes de la première défintiion.

1) Deux triangles sont semblables si et seulement si leurs angles sont identiques (congrus).

2) Deux triangles sont semblables si et seulement si les rapports de leurs cotés homologues sont identiques (congrus).

Propriétés

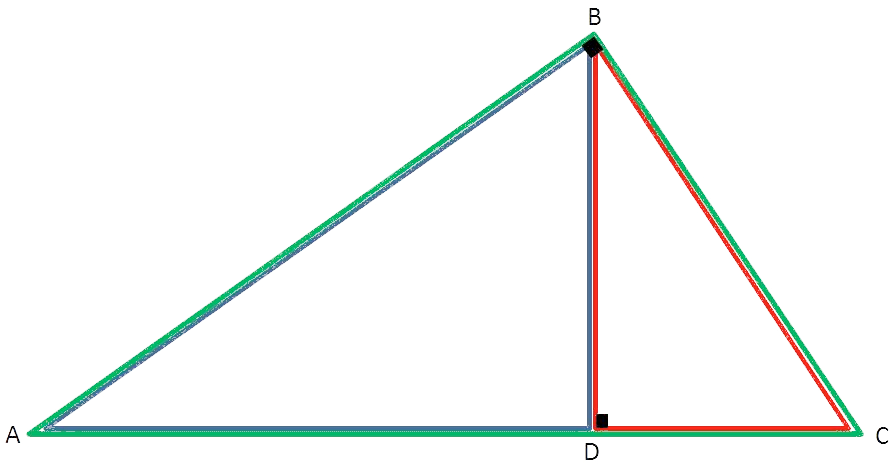
\[\frac{\color {blue} \Delta ADB}{\color {green} \Delta ABC} : \frac{\color {blue}mAB}{\color {green}mAC} = \frac{\color {blue}mAD}{\color {green}mAB} = \frac{\color {blue}mDB}{\color {green}mBC}\]

\[\frac{\color {red} \Delta BDC}{\color {green} \Delta ABC} : \frac{\color {red}mBC}{\color {green}mAC} = \frac{\color {red}mBD}{\color {green}mAB} = \frac{\color {red}mDC}{\color {green}mBC}\]

\[\frac{\color {blue} \Delta ADB}{\color {red} \Delta BDC} : \frac{\color {blue}mAB}{\color {red}mBC} = \frac{\color {blue}mAD}{\color {red}mBD} = \frac{\color {blue}mDB}{\color {red}mDC}\]